DAL BIT AL QUBIT

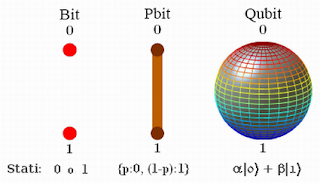
L’entità fondamentale dell’informatica è il "bit", ovvero un sistema, ad esempio un condensatore, che può assumere due valori ben distinti, che si indicano con "0", condensatore scarico, oppure "1", condensatore carico. Mediante una successione ordinata di bit è possibile codificare dell’informazione. L’esempio più semplice è la codifica binaria di un qualsiasi numero decimale con una successione ben determinata di 0 e di 1; così, ad esempio, il numero decimale 5 si scrive in codifica binaria 101, il numero 17 si scrive 10001. La controparte quantistica del bit è il "qubit" o "bit quantistico". Così come per il bit, il qubit è un sistema a due livelli, i cui stati sono indicati semplicemente con | 0 >, ket 0, e | 1 >, ket 1, che soddisfano alle seguenti proprietà:

< 0 | 0 > = 1, < 1 | 1 > = 1, < 0 | 1 > = 0,  < 1 | 0 > = 0, 

ove < | si legge "bra", duale dell'operatore "ket".
In questo modo un fotone o un atomo possono essere visti come dei qubit, quindi: qubit nello stato | 0 > equivale a supporre il fotone con polarizzazione orizzontale | H > oppure l'atomo nello stato fondamentale | f >, qubit nello stato | 1 > si può immaginare il fotone con polarizzazione verticale | V > o l'atomo nello stato eccitato | e >.
Mentre il bit può assumere solo uno dei due valori possibili, "0" o "1", il qubit può trovarsi nello stato | 0 > o | 1 >, oppure in infiniti stati di sovrapposizione del tipo:

| ψ > = a | 0 > + b | 1 >,

con le infinite combinazioni di a, b appartenenti al campo dei numeri reali R tali che a² + b² = 1. Un qubit del tipo descritto è sia "0" che "1" con probabilità determinate dalle leggi della meccanica quantistica. Questo ha importanti ripercussioni nella computazione quantistica.
Si considerino, ora, due qubit; escludendo gli stati di sovrapposizione, abbiamo quattro possibili stati ai quali si possono assegnare, ad esempio, quattro numeri decimali passando dalla codifica binaria, come mostrato di seguito:
1) | 0 >₁ | 0 >₂ ≡ numero binario 00 ≡ numero decimale 0;
2) | 0 >₁ | 1 >₂ ≡ numero binario 01 ≡ numero decimale 1;
3) | 1 >₁ | 0 >₂ ≡ numero binario 10 ≡ numero decimale 2;
4) | 1 >₁ | 1 >₂ ≡ numero binario 11 ≡ numero decimale 3.
Come nel caso del singolo qubit, anche per due qubit si possono considerare stati di sovrapposizione del tipo:

| ψ >₁₂ = a | 0 >₁ | 0 >₂ + b | 0 >₁ | 1 >₂ + c | 1 >₁ | 0 >₂ + d | 1 >₁ | 1 >₂,

con a² + b² + c² + d² = 1 e a, b, c, d appartenenti al campo dei numeri reali R.
Nell’esistenza degli stati di sovrapposizione risiedono le principali potenzialità della meccanica quantistica e, in particolare, dell'informatica quantistica: la computazione può essere eseguita in maniera esponenzialmente più veloce impiegando stati quantistici anziché semplici mezzi classici.
Quindi la potenza del calcolo quantistico risiede nell’esistenza delle sovrapposizioni quantistiche, in questo modo si possono eseguire operazioni in parallelo con un solo passaggio (parallelismo quantistico).